Data Structure and Algorithms in Python
Chapter 1 - Python Primer
-
Python’s syntax relies heavily on the use of
whitespace. Individual statements are typically concluded with anewlinecharacter, although a command can extend to another line, either with a concludingbackslash character (\), or if an opening delimiter has not yet been closed, - Python treats everything as
object. - Python automatically chooses the internal representation for an integer based upon the magnitude of its value.
-
By default, the string must use base 10. If conversion from a different base is desired, that base can be indicated as a second, optional, parameter. For example, the expression
int( 7f , 16)evaluates to the integer127. - To express
a tuple of length one as a literal, a comma must be placed after the element, but
within the parentheses. For example,
(17,)is a one-element tuple. The reason for this requirement is that, without the trailing comma, the expression(17)is viewed as a simple parenthesized numeric expression. - Alternatively, the quote delimiter can be designated using a
backslash as a so-called escape character, as in
Don\'t worry. Because the backslash has this purpose, the backslash must itself be escaped to occur as a natu- ral character of the string literal, as inC:\\Python\\, for a string that would be displayed asC:\Python\. - The first is that the
setdoes not maintain the elements in any particular order. The second is that only instances ofimmutabletypes can be added to a Python set. Therefore, objects such as integers, floating-point numbers, and character strings are eligible to be elements of a set. - Python uses curly braces
{ and }as delimiters for a set, for example, as{17}or{ red , green , blue }. Theexceptionto this rule is that{ }does not represent anempty set; for historical reasons, it represents anempty dictionary(see next paragraph). Instead, the constructor syntaxset( )produces an empty set. -
If an iterable parameter is sent to the constructor
set(), then the set of distinct elements is produced. For example,set("hello")produces{'h','e','l','l','o'}. -
The constructor for the
dictclass accepts an existing mapping as a parameter, in which case it creates a new dictionary with identical associations as the existing one. Alternatively, the constructor accepts a sequence of key-value pairs as a parameter, as indict(pairs)withpairs = [('ga','Irish'), ('de','German')]. - The
andandoroperatorsshort-circuit, in that they do not evaluate the second operand if the result can be determined based on the value of the first operand. This feature is useful when constructing Boolean expressions in which we first test that a certain condition holds (such as a reference not being None), and then test a condition that could have otherwise generated an error condition had the prior test not succeeded. -
The expression
a is bevaluates toTrue, precisely when identifiersaandbarealiasesfor the same object. The expressiona == btests a more general notion ofequivalence. If identifiersaandbrefer to the same object, thena == bshould also evaluate toTrue. Yeta == balso evaluates toTruewhen the identifiers refer to different objects that happen to have values that are deemed equivalent. The precise notion of equivalence depends on the data type. For example, two strings are considered equivalent if they match character for character. Two sets are equivalent if they have the same contents, irrespective of order. In most programming situations, the equivalence tests==and!=are the appropriate operators; use ofisandis notshould be reserved for situations in which it is necessary to detect true aliasing. - In Python, the
/operator designatestruedivision, returning thefloating-pointresult of the computation. Thus,27 / 4results in the float value6.75. Python supports the pair of operators//and%to perform the integral calculations, with expression27 // 4evaluating to int value6(the mathematical floor of the quotient), and expression27 % 4evaluating to int value3, the remainder of the integer division. - Python carefully extends the semantics of
//and%to cases where one or both operands arenegative. For the sake of notation, let us assume that variablesnandmrepresent respectively thedividendanddivisor.q = n // mandr = n % m. Python guarantees thatq m + rwill equaln. We already saw an example of this identity with positive operands, as 6 ∗ 4 + 3 = 27. When the divisormis positive, Python further guarantees that0 ≤ r < m. As a consequence, we find that−27 // 4evaluates to−7and−27 % 4evaluates to1, as(−7) ∗ 4 + 1 = −27. When the divisor is negative, Python guarantees thatm < r ≤ 0. As an example,27 // −4is−7and27 % −4is−1, satisfying the identity27 = (−7) ∗ (−4) + (−1). -
The conventions for the
//and%operators are even extended to floating- point operands, with the expressionq = n // mbeing the integral floor of the quotient, andr = n % mbeing the “remainder” to ensure thatq m + requals n. For example,8.2 // 3.14evaluates to2.0and8.2 % 3.14evaluates to1.92, as2.0 ∗ 3.14 + 1.92 = 8.2. - Bitwise operations
~ bitwise complement (prefix unary operator) & bitwise and | bitwise or ˆ bitwise exclusive-or << shift bits left, filling in with zeros >> shift bits right, filling in with sign bit - Sequence Operators
- Each of Python’s built-in sequence types (str, tuple, and list) support the following operator syntaxes:
s[j] element at index j
s[start:stop] slice including indices [start,stop)
s[start:stop:step] slice including indices start, start + step,
start + 2 step, . . . , up to but not equalling or stop
s+t concatenation of sequences
s*k shorthand for s + s + s + ... (k times)
val in s containment check
val not in s non-containment check
- Operators for Sets and Dictionaries
Setsandfrozensetssupport the following operators:key in s containment check key not in s non-containment check s1 == s2 s1 is equivalent to s2 s1 != s2 s1 is not equivalent to s2 s1 <= s2 s1 is subset of s2 s1 < s2 s1 is proper subset of s2 s1 >= s2 s1 is superset of s2 s1 > s2 s1 is proper superset of s2 s1 | s2 the union of s1 and s2 s1 & s2 the intersection of s1 and s2 s1 − s2 the set of elements in s1 but not s2 s1 ˆ s2 the set of elements in precisely one of s1 or s2
- Extended assignment operator:
alpha = [1, 2, 3] beta = alpha # an alias for alpha beta += [4, 5] # extends the original list with two more elements beta = beta + [6, 7] # reassigns beta to a new list [1, 2, 3, 4, 5, 6, 7] print(alpha) # will be [1, 2, 3, 4, 5] - Python fuctions uses
pass by referencenotpass by value. An advantage to Python’s mechanism for passing information to and from a function is thatobjectsare not copied. This ensures that the invocation of a function is efficient, even in a case where a parameter or return value is a complex object. -
We note that reassigning a new value to a formal parameter with a function body, such as by setting
data = [ ], does not alter the actual parameter; such a reassignment simply breaks the alias. -
In
print()The separator can be customized by providing a desired separating string as a keyword parameter,sep. For example, colon separated output can be produced asprint(a, b, c, sep=':' ). -
By default, a trailing newline is output after the final argument. An alternative trailing string can be designated using a keyword parameter,
end. Designating the empty stringend=''suppresses all trailing characters. - File operation functions.
fp.seek(k): Change the current position to be at the k th byte of the file.fp.tell( ): Return the current position, measured as byte-offset from the start.
- Exception Hierarchy.
- Exception
- AttributeError
- EOFError
- IOError
- IndexError
- KeyError
- KeyboardInterrupt
- NameError
- StopIteration
- TypeError
- ValueError
- ZeroDivisionError
-
A second philosophy, often embraced by Python programmers, is that
“It is easier to ask for forgiveness than it is to get permission.”
In Python, this philosophy is implemented using a try-except control structure. - The keyword,
pass, is a statement that does nothing, yet it can serve syntactically as a body of a control structure. -
A
try-statement can have afinallyclause, with a body of code that will always be executed in the standard or exceptional cases, even when an uncaught or re-raised exception occurs. That block is typically used for critical cleanup work, such as closing an open file. - An iterator is an object that manages an iteration through a series of values. If
variable,
i, identifies an iterator object, then each call to the built-in function,next(i), produces a subsequent element from the underlying series, with a StopIteration exception raised to indicate that there are no further elements. -
An iterable is an object, obj, that produces an iterator via the syntax
iter(obj). - By these definitions, an instance of a list is an iterable, but not itself an iterator.
With
data = [1, 2, 4, 8], it is not legal to callnext(data). However, an iterator object can be produced with syntax,i = iter(data), and then each subsequent call tonext(i)will return an element of that list. -
Use of the keyword
yieldrather thanreturnto indicate a result. This indicates to Python that we are defining agenerator, rather than a traditional function. -
expr1 if condition else expr2This compound expression evaluates toexpr1if the condition is true, and otherwise evaluates toexpr2. For those familiar with Java or C++, this is equivalent to the syntax,condition ? expr1 : expr2, in those languages. - Comprehensions.
[ k k for k in range(1, n+1) ]list comprehension{ k k for k in range(1, n+1) }set comprehension( k k for k in range(1, n+1) )generator comprehension{ k : k k for k in range(1, n+1) }dictionary comprehension
- Methods of RANDOM class.
seed(hashable): Initializes the pseudo-random number generator based upon the hash value of the parameterrandom( ): Returns a pseudo-random floating-point value in the interval [0.0, 1.0).randint(a,b): Returns a pseudo-random integer in the closed interval [a, b].randrange(start, stop, step): Returns a pseudo-random integer in the standard Python range indicated by the parameters.choice(seq): Returns an element of the given sequence chosen pseudo-randomly.shuffle(seq): Reorders the elements of the given sequence pseudo-randomly.
Chapter 2 - OOP in Python
Special methods for Class.
a + b : a.__add__(b);
a - b : a.__sub__(b);
a * b : a.__mul__(b);
a / b : a.__truediv__(b);
a // b : a.__floordiv__(b);
a % b : a.__mod__(b);
a ** b : a.__pow__(b);
a << b : a.__lshift__(b);
a >> b : a.__rshift__(b);
a & b : a.__and__(b);
a ^ b : a.__xor__(b);
a | b : a.__or__(b);
a += b : a.__iadd__(b)
a -= b : a.__isub__(b)
a *= b : a.__imul__(b)
etc...
+a : a.__pos__( )
-a : a.__neg__( )
~a : a.__invert__( )
abs(a) : a.__abs__( )
a < b : a.__lt__(b)
a <= b : a.__le__(b)
a > b : a.__gt__(b)
a >= b : a.__ge__(b)
a == b : a.__eq__(b)
a != b : a.__ne__(b)
v in a : a.__contains__(v)
a[k] : a.__getitem__(k)
a[k] = v : a.__setitem__(k,v)
del a[k] : a.__delitem__(k)
a(arg1, arg2, ...): a.__call__(arg1, arg2, ...)
len(a) : a.__len__( )
hash(a) : a.__hash__( )
iter(a) : a.__iter__( )
next(a) : a.__next__( )
bool(a) : a.__bool__( )
float(a) : a.__float__( )
int(a) : a.__int__( )
repr(a) : a.__repr__( )
reversed(a) : a.__reversed__( )
str(a) : a.__str__( )
Copy module of python
This module supports two functions: the copy function creates a shallow copy
of its argument, and the deepcopy function creates a deep copy of its argument.
After importing the module, we may create a deep copy for any object as follows:
palette = copy.deepcopy(warmtones)
Chapter 3 - Algorithm Analysis
Big-Oh Notation:
Let f(n) and g(n) be functions mapping positive integers to positive real numbers.
We say that f(n) is O(g(n)) if there is a real constant c > 0 and an integer constant
n0 ≥ 1 such that,
f(n) ≤ cg(n), for n ≥ n0
Big-Omega Notation
Just as the big-Oh notation provides an asymptotic way of saying that a function is
less than or equal to another function, the following notations provide an asymptotic way of saying that a function grows at a rate that is greater than or equal to
that of another.
Let f(n) and g(n) be functions mapping positive integers to positive real numbers. We say that f(n) is Ω(g(n)), pronounced
f(n) is big-Omega of g(n)
if g(n) is O(f(n)), that is, there is a real constant c > 0 and an integer constant n0 ≥ 1 such that,
f(n) ≥ cg(n), for n ≥ n0.
Big-Theta Notation
In addition, there is a notation that allows us to say that two functions grow at the
same rate, up to constant factors. We say that f(n) is Θ(g(n)), pronounced f(n) is big-Theta of g(n) if f(n) is O(g(n)) and f(n) is Ω(g(n)) , that is, there are real
constants c1 > 0 and c2 > 0, and an integer constant n0 ≥ 1 such that,
c1 g(n) ≤ f(n) ≤ c2 g(n), for n ≥ n0.
Chapter 4 - Recursion
- Python interpreter can be dynamically reconfigured to change
the default recursive limit. This is done through use of a module named sys, which
supports a
getrecursionlimitfunction and asetrecursionlimit. Sample usage of those functions is demonstrated as follows:import sys old = sys.getrecursionlimit( ) # perhaps 1000 is typical sys.setrecursionlimit(1000000) # change to allow 1 million nested calls
Chapter 5 - Array-Based Sequences
- Python internally represents each
Unicode character with
16 bits(i.e., 2 bytes). Therefore, a six-character string, such as SAMPLE , would be stored in12consecutive bytes of memory. - Python represents a list or tuple instance using an internal storage mechanism of an array of object references. At the lowest level, what is stored is a consecutive sequence of memory addresses at which the elements of the sequence reside.
- Although the relative size of the individual elements may vary, the number of bits used to store the memory address of each element is fixed (e.g., 64-bits per address).
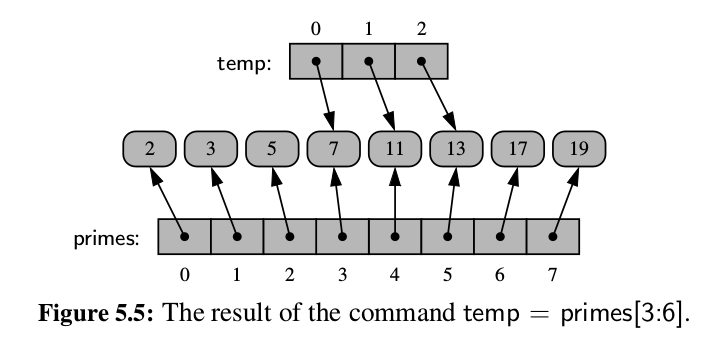
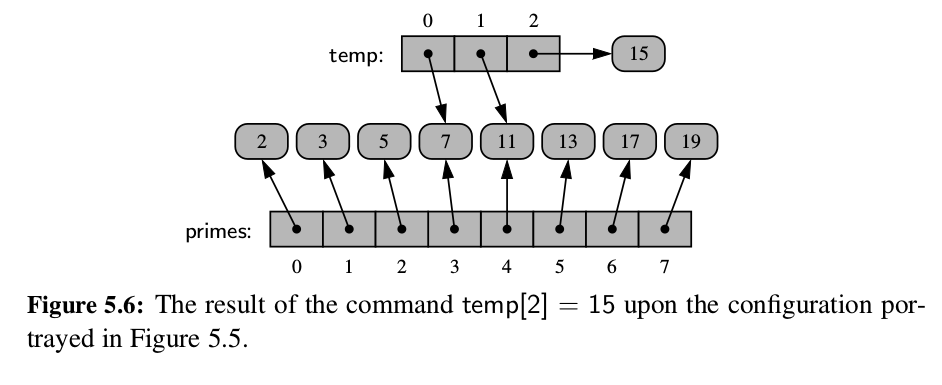
- When you compute a slice of a list, the result is a new
list instance, but that new list has references to the same elements that are in the
original list.
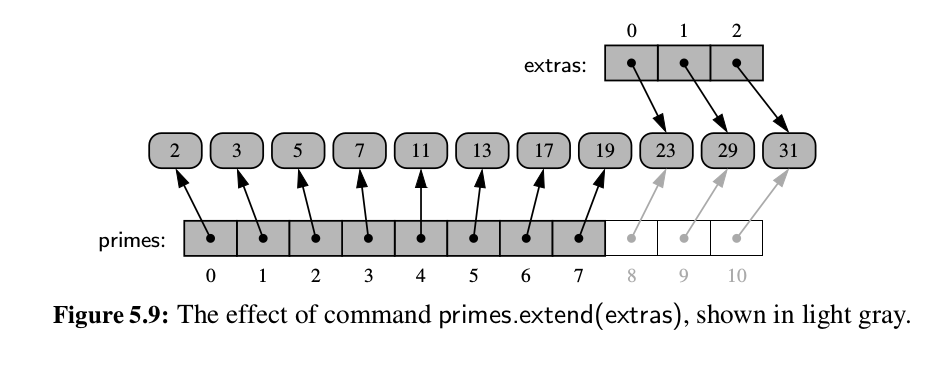
Images below shows some of properties of list.
 ———————————————————————————————-
———————————————————————————————-
 ———————————————————————————————-
———————————————————————————————-
 ———————————————————————————————-
———————————————————————————————-
 ———————————————————————————————-
———————————————————————————————-
 ———————————————————————————————-
———————————————————————————————-
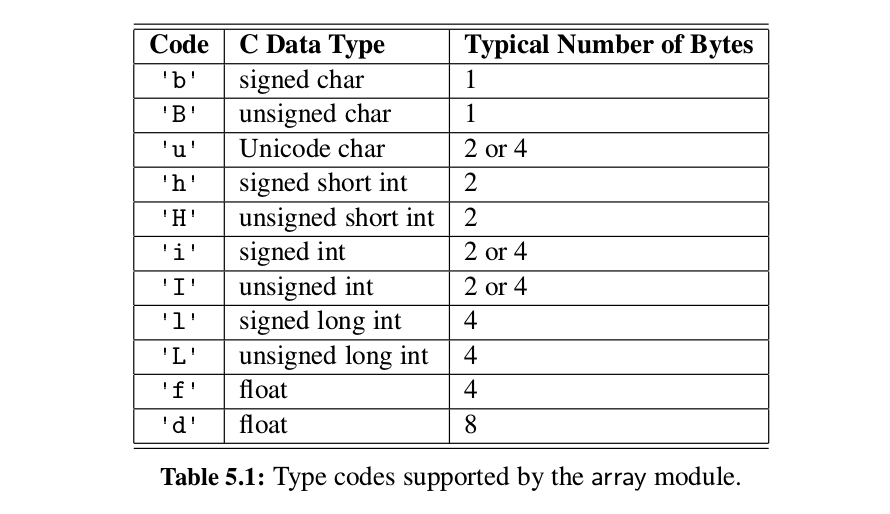
- Primary support for compact arrays is in a module named
array. That module defines a class, also namedarray, providing compact storage for arrays of primitive data types. - The constructor for the array class requires a type code as a first parameter,
which is a character that designates the type of data that will be stored in the array.
As a tangible example, the type code,
i, designates an array of (signed) integers, typically represented using at least 16-bits each.primes = array( i , [2, 3, 5, 7, 11, 13, 17, 19]) - The type code allows the interpreter to determine precisely how many bits are
needed per element of the array. The type codes supported by the
arraymodule, as shown in Table 5.1.
- Python’s list class presents a more interesting abstraction. Although a list has a
particular length when constructed, the class allows us to add elements to the list,
with no apparent limit on the overall capacity of the list. To provide this abstraction,
Python relies on an algorithmic sleight of hand known as a dynamic array.
The first key to providing the semantics of a dynamic array is that a list instance maintains an underlying array that often has greater capacity than the current length of the list. For example, while a user may have created a list with five elements, the system may have reserved an underlying array capable of storing eight object references (rather than only five). This extra capacity makes it easy to append a new element to the list by using the next available cell of the array.
If a user continues to append elements to a list, any reserved capacity will eventually be exhausted. In that case, the class requests a new, larger array from the system, and initializes the new array so that its prefix matches that of the existing smaller array. At that point in time, the old array is no longer needed, so it is reclaimed by the system. Intuitively, this strategy is much like that of the hermit crab, which moves into a larger shell when it outgrows its previous one.
Tuples and Strings

Lists

- In practice, the extend method is preferable to repeated calls to append because
the constant factors hidden in the asymptotic analysis are significantly smaller. The
greater efficiency of extend is threefold.
Finally, increased efficiency of extend comes from the fact that the resulting size of the updated list can be calculated in advance. If the second data set is quite large, there is some risk that the underlying dynamic array might be resized multiple times when using repeated calls to append. With a single call to extend, at most one resize operation will be performed. - Experiments should show that the list comprehension syntax is significantly faster than building the list by repeatedly appending.
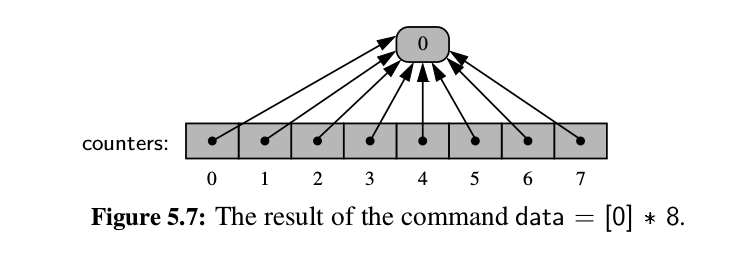
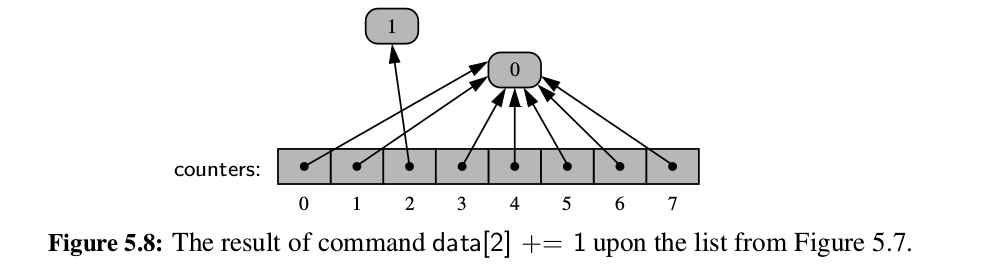
- It is a common Python idiom to initialize a list of constant values
using the multiplication operator, as in
[0]*nto produce a list of length n with all values equal to zero. Not only is this succinct for the programmer; it is more efficient than building such a list incrementally.
Strings
- The analysis for many behaviors is quite intuitive. For example, methods that produce a new string (e.g., capitalize, center, strip) require time that is linear in the length of the string that is produced. Many of the behaviors that test Boolean conditions of a string (e.g., islower) take O(n) time, examining all n characters in the worst case, but short circuiting as soon as the answer becomes evident (e.g., islower can immediately return False if the first character is uppercased). The comparison operators (e.g., ==, <) fall into this category as well.
Chapter 6 - Stacks, Queues, and Deques
Stack
- A stack is a collection of objects that are inserted and removed according to the last-in, first-out (LIFO) principle. A user may insert objects into a stack at any time, but may only access or remove the most recently inserted object that remains (at the so-called “top” of the stack).
- Following methods are supported by
stackADT.S.push(e): Add element e to the top of stack S.S.pop( ): Remove and return the top element from the stack S; an error occurs if the stack is empty.S.top( ): Return a reference to the top element of stack S, without removing it; an error occurs if the stack is empty.S.is empty( ): Return True if stack S does not contain any elements.len(S): Return the number of elements in stack S;
- Realization of a stack S as an adaptation of a Python list L.
| Stack Method | Realization with Python list |
|---|---|
| S.push(e) | L.append(e) |
| S.pop( ) | L.pop() |
| S.top( ) | L[-1] |
| S.is_empty( ) | len(L) == 0 |
| len(S) | len(L) |
-
S.push(e)andS.pop( )has amortized cost ofO(1).S.top( ),S.is_empty( ),len(S)has cost ofO(1). -
Following Exception is used when we want to raise empty Exception.
class Empty(Exception):
”””Error attempting to access an element from an empty container.”””
pass
- Implementation of Stack as Python ADT class.
class ArrayStack:
"""LIFO Stack implementation using a Python list as underlying storage."""
def __init__(self):
"""Create an empty stack."""
self._data = [] # nonpublic list instance
def __len__(self):
"""Return the number of elements in the stack."""
return len(self._data)
def is_empty(self):
"""Return True if the stack is empty."""
return len(self._data) == 0
def push(self, e):
"""Add element e to the top of the stack."""
self._data.append(e) # new item stored at end of list
def top(self):
"""Return (but do not remove) the element at the top of the stack.
Raise Empty exception if the stack is empty.
"""
if self.is_empty():
raise Empty('Stack is empty')
return self._data[-1] # the last item in the list
def pop(self):
"""Remove and return the element from the top of the stack (i.e., LIFO).
Raise Empty exception if the stack is empty.
"""
if self.is_empty():
raise Empty('Stack is empty')
return self._data.pop() # remove last item from list
if __name__ == '__main__':
S = ArrayStack() # contents: [ ]
S.push(5) # contents: [5]
S.push(3) # contents: [5, 3]
print(len(S)) # contents: [5, 3]; outputs 2
print(S.pop()) # contents: [5]; outputs 3
print(S.is_empty()) # contents: [5]; outputs False
print(S.pop()) # contents: [ ]; outputs 5
print(S.is_empty()) # contents: [ ]; outputs True
S.push(7) # contents: [7]
S.push(9) # contents: [7, 9]
print(S.top()) # contents: [7, 9]; outputs 9
S.push(4) # contents: [7, 9, 4]
print(len(S)) # contents: [7, 9, 4]; outputs 3
print(S.pop()) # contents: [7, 9]; outputs 4
S.push(6) # contents: [7, 9, 6]
S.push(8) # contents: [7, 9, 6, 8]
print(S.pop()) # contents: [7, 9, 6]; outputs 8
Queues
- Another fundamental data structure is the queue. It is a close “cousin” of the stack, as a queue is a collection of objects that are inserted and removed according to the first-in, first-out (FIFO) principle.
- Following methods are supported by
queueADT.Q.enqueue(e): Add element e to the back of queue Q.Q.dequeue( ): Remove and return the first element from queue Q; an error occurs if the queue is empty.Q.first( ): Return a reference to the element at the front of queue Q, without removing it; an error occurs if the queue is empty.Q.is_empty( ): Return True if queue Q does not contain any elements.len(Q): Return the number of elements in queue Q;
- Implementation of Queues as python ADT class.
class ArrayQueue:
"""FIFO queue implementation using a Python list as underlying storage."""
DEFAULT_CAPACITY = 10 # moderate capacity for all new queues
def __init__(self):
"""Create an empty queue."""
self._data = [None] * ArrayQueue.DEFAULT_CAPACITY
self._size = 0
self._front = 0
def __len__(self):
"""Return the number of elements in the queue."""
return self._size
def is_empty(self):
"""Return True if the queue is empty."""
return self._size == 0
def first(self):
"""Return (but do not remove) the element at the front of the queue.
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
return self._data[self._front]
def dequeue(self):
"""Remove and return the first element of the queue (i.e., FIFO).
Raise Empty exception if the queue is empty.
"""
if self.is_empty():
raise Empty('Queue is empty')
answer = self._data[self._front]
self._data[self._front] = None # help garbage collection
self._front = (self._front + 1) % len(self._data)
self._size -= 1
return answer
def enqueue(self, e):
"""Add an element to the back of queue."""
if self._size == len(self._data):
self._resize(2 * len(self.data)) # double the array size
avail = (self._front + self._size) % len(self._data)
self._data[avail] = e
self._size += 1
def _resize(self, cap): # we assume cap >= len(self)
"""Resize to a new list of capacity >= len(self)."""
old = self._data # keep track of existing list
self._data = [None] * cap # allocate list with new capacity
walk = self._front
for k in range(self._size): # only consider existing elements
self._data[k] = old[walk] # intentionally shift indices
walk = (1 + walk) % len(old) # use old size as modulus
self._front = 0 # front has been realigned
Double-Ended Queues
-
We next consider a queue-like data structure that supports insertion and deletion at both the front and the back of the queue. Such a structure is called a double- ended queue, or
deque, which is usually pronounced “deck” to avoid confusion with the dequeue method of the regular queue ADT, which is pronounced like the abbreviation “D.Q.” - Following methods are supported by
dequeADT.D.add first(e): Add element e to the front of deque D.D.add last(e): Add element e to the back of deque D.D.delete first( ): Remove and return the first element from deque D; an error occurs if the deque is empty.D.delete last( ): Remove and return the last element from deque D; an error occurs if the deque is empty.D.first( ): Return (but do not remove) the first element of deque D; an error occurs if the deque is empty.D.last( ): Return (but do not remove) the last element of deque D; an error occurs if the deque is empty.D.is_empty( ): Return True if deque D does not contain any elements.len(D): Return the number of elements in deque D;
- An implementation of a
dequeclass is available in Python’s standardcollectionsmodule.
Chapter 7 - Linked List
Link-Based vs. Array-Based Sequences
Advantages of Array-Based Sequences- Arrays provide
O(1)-time access to an element based on an integer index. The ability to access the k th element for any k inO(1)time is a hallmark advantage of arrays. In contrast, locating the k th element in a linked list requiresO(k)time to traverse the list from the beginning, or possiblyO(n − k)time, if traversing backward from the end of a doubly linked list. - Array-based representations typically use proportionally less memory than
linked structures. This advantage may seem counterintuitive, especially given
that the length of a dynamic array may be longer than the number of elements
that it stores. Both array-based lists and linked lists are referential structures,
so the primary memory for storing the actual objects that are elements is the
same for either structure. What differs is the auxiliary amounts of memory
that are used by the two structures. For an array-based container of n elements,
a typical worst case may be that a recently resized dynamic array has
allocated memory for
2nobject references. With linked lists, memory must be devoted not only to store a reference to each contained object, but also explicit references that link the nodes. So a singly linked list of lengthnalready requires2nreferences (an element reference and next reference for each node). With a doubly linked list, there are3nreferences.
- Arrays provide
Advantages of Link-Based Sequences- Link-based structures provide worst-case time bounds for their operations. This is in contrast to the amortized bounds associated with the expansion or contraction of a dynamic array. When many individual operations are part of a larger computation, and we only care about the total time of that computation, an amortized bound is as good as a worst-case bound precisely because it gives a guarantee on the sum of the time spent on the individual operations. However, if data structure operations are used in a real-time system that is designed to provide more immediate responses (e.g., an operating system, Web server, air traffic control system), a long delay caused by a single (amortized) operation may have an adverse effect.
- Link-based structures support
O(1)-time insertions and deletions at arbitrary positions. This is in stark contrast to an array-based sequence. Ignoring the issue of resizing an array, inserting or deleting an element from the end of an array- based list can be done in constant time. However, more general insertions and deletions are expensive. For example, with Python’s array-based list class, a call to insert or pop with indexkusesO(n − k + 1)time because of the loop to shift all subsequent elements. As an example application, consider a text editor that maintains a document as a sequence of characters. Although users often add characters to the end of the document, it is also possible to use the cursor to insert or delete one or more characters at an arbitrary position within the document. If the character sequence were stored in an array-based sequence (such as a Python list), each such edit operation may require linearly many characters to be shifted, leading toO(n)performance for each edit operation. With a linked-list representation, an arbitrary edit operation (insertion or deletion of a character at the cursor) can be performed inO(1)worst-case time, assuming we are given a position that represents the location of the cursor.
Chapter 8 - Trees
- Accessor methods of the Tree ADT
| T.root( ) | Return the position of the root of tree T, or None if T is empty. |
| T.is root(p) | Return True if position p is the root of Tree T. |
| T.parent(p) | Return the position of the parent of position p, or None if p is the root of T. |
| T.num children(p) | Return the number of children of position p. |
| T.children(p) | Generate an iteration of the children of position p. |
| T.is leaf(p) | Return True if position p does not have any children. |
| len(T) | Return the number of positions (and hence elements) that are contained in tree T. |
| T.is empty( ) | Return True if tree T does not contain any positions. |
| T.positions( ) | Generate an iteration of all positions of tree T. |
| iter(T) | Generate an iteration of all elements stored within tree T. |
- Tree Traversals:
- Inorder (Left, Root, Right)
- Preorder (Root, Left, Right)
- Postorder (Left, Right, Root)
- BFS